By - Chris Winters

Note by the editor R. Styma.
While Round and Round Magazine is no longer in publication, the contents of this article are still valuable.

The current rules of scoring are the same as described in this series of articles, but the colored pencils have been replaced with computer printouts and the application of the rules is performed using a computer. At the National Championship, scores are entered by the judges via computer and also written down. What is entered into the computer is the master copy. The judge keeps their score sheets for reference. At other contests, the raw scores are written down by the judges onto score sheets and entered into the computer by the tabulator. In all cases, the scoring program in the computer then applies the eleven rules described here to determine the placements in the event.

The tabulating sheet (TAB Sheet) has been replaced by the USARS Summary sheet which contains the same information with the addition of the Skaters Name. This improves the longevity of the sheet showing your first big win. Do you really remember your contestant number at Nationals in 1995? The USARS summary also shows the contestants in order of placement rather than skating order. The skating order is stored as the last column on the right.

The text of "The Scoreboard" has been left in its original form.

Part I

Consistent with the new publishers philosophy of "Informed Skaters are Better Skaters." a six (6) part series on the principles of Competitive Artistic Scoring will be published during future issues. It is hoped that the information provided will help those who have looked over the complicated score sheets and wondered what in the world it all means. While at numerous local, regional, and national events, I have stood behind skaters and spectators looking at a posted score sheet and overheard them saying, "How do they figure we got 15^th place?" or "Johnny got 8^th place" (While pointing at the M.O. figure) when in fact Johnny was holding 10^th place. The inability to read the score sheet correctly very often leads to irritation and disillusionment.

It is hoped that from the information to be provided in this and future issues, readers will be able to read and understand the various numbers on the score sheet and how they are obtained. The work of scoring, tabulating, and processing of statistics is one of the most important and exacting phases of competitive skating. For this reason, USAS has published a book entitled Tabulating and Scoring Manual that provides a detailed outline of the scoring process.

Part II, which includes a description of the judge score entry and ordinaling, will appear in the next issue of Round and Round.

Part II

This article is Part II of a six part series on the principles of competitive artistic scoring. Part I may be found in the Vol. 20 issue of Round and Round.

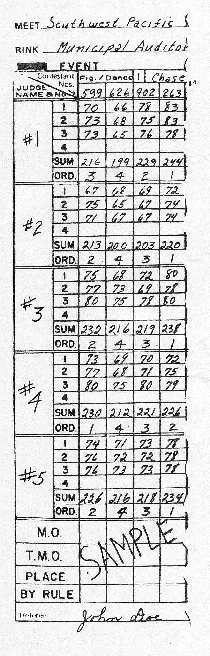
USAC judges grade each performance by awarding the contestant a score in the range of 0 to 100 (perfect) dependent upon the caliber of the skating demonstrated. In dance and figure events where 3 for 4 scores are assigned according to the number of dances or figures skated, the judge's score for the first dance/figure skated is recorded, using a black lead pencil, on the USAC General Score Sheet in the proper space on line 1 opposite that judge's name or number. The second score is for the second dance/figure skated and is recorded in the proper space on line 2. In like manner, the third and fourth scores are recorded. The above procedure will also be used for recording the judge's scores for execution and content of a contestant's performance of a freestyle event. For an example of score entries, see the sample score sheet. Contests where only one score is assigned by each judge, such as the Dance of the Month contest, only one entry will be made.

Looking at the sample score sheet, you will notice that below line 4 for each judge is a line marked SUM. The SUM is a number obtained by adding the entries or scores recorded in lines 1 through 4 mentioned above and represents the total score/points the contestant received from that individual judge for all the dances/figures skated. In a freestyle event, it represents the total score/points the contestant received from that judge for the overall performance. If only one score entry is made, such as the Dance of the Month contest, this entry will likewise be the SUM and most often will only appear on the SUM line. A blue pencil is used to make the SUM entry on the score sheet.

Below the SUM line, for each judge is a line marked ORD (ordinal) . The ORD is a number indicating an individual judge's choice or placement for each contestant who has competed in the event. The ordinal number is assigned in accordance with each contestant's SUM. The contestant with the highest numerical SUM will receive an ORD or 1. The contestant with the next highest numerical SUM will receive an ORD or 2. This process continues until the contestant with the lowest numerical SUM receives and ORD number equal to the number of contestants skating. The ORD entry is made using a red pencil.

In Part III, which will appear in the next issue of Round and Round, we will cover the method of obtaining the Majority Ordinal (MO) and the application of the first rules for awarding placements. The Majority Ordinal is probably the one number that creates the most confusion and misunderstanding. Read the next issue and get a good understanding of the MO number.

Part III

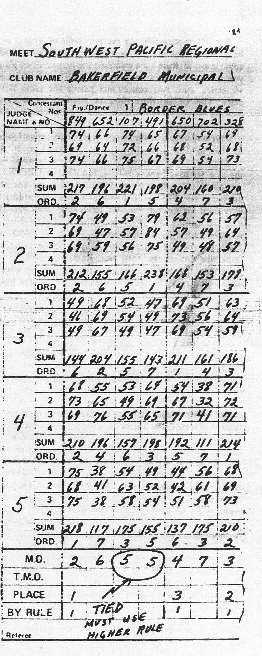In Part II we saw that the ORDINAL assigned to a sum indicated that the judge's choice of placement for the skater or team who competed in the event. The sample score sheet in Part II showed ordinals assigned to the SUM for each judge. This is easy and understandable thus far; but how do we establish an overall placement from all these ordinals? Here is where the majority ordinal (MO) comes into play. As mentioned in part II, the majority ordinal is probably the one number on the score sheet that creates the most confusion and misunderstanding. It is hoped that the following explanation will help clarify the meaning and use of MO.

A majority ordinal is a number indicating the highest place for which a contestant has a majority. Or to put it another way, the MO is the median or middle ordinal of all the individual judge's ordinals. As an example suppose a contestant has ordinals of 1, 2, 6, 5, and 7 in a contest of five judges. Here the majority ordinal is 5, since 5 is the medium or middle ordinal. The MO is taken from the best 3 out of 5 ordinals. In this case, two judges felt that the contestant should have a placement higher than fifth and two felt the placement should have been lower than fifth. What if the ordinals would have been 1, 1, 4, 4, and 4 instead of those shown above. In this case the MO would have been 4 because, again it is the middle ordinal. Here is an easy way to select the MO from a set of ordinals. In the case of a contest with five judges, you would select the highest ordinal from the three lowest ordinals. For a contest with three judges, you would select the highest ordinal from the two lowest ones. By using this process you will be selecting the middle or medium ordinal.

A majority ordinal is assigned to each contestant competing in the event and is entered in the proper space on the MO line just below the last judge's entry. The MO number is entered on the score sheet with green pencil. In order to test your understanding of the MO selection process, try following the MO assignments made on the sample score sheet.

After selecting the MO for each contestant, the process of awarding the highest open placement is started. The first highest placements to be awarded is the traditional first place, Followed by the second place and then the third, etc. The procedure for awarding placements begins with Rule 1. This rule states that the highest open place shall be awarded to the contestant with the lowest majority ordinal, which is the MO we selected using the process mentioned above. Simply, this means that after selecting and entering the MO's for all contestants, we would make a visual comparison of all these MO's and the contestant with the lowest MO would receive first place. The contestant with the next lowest MO would receive second place and so on until we find two or more contestants with the same MO. This is considered a tie and requires additional computation for breaking. These additional computations will be the subject material of Part IV to be published in the next issue of Round and Round. Be sure to get our copy and follow the tie breaking rules.

Part IV

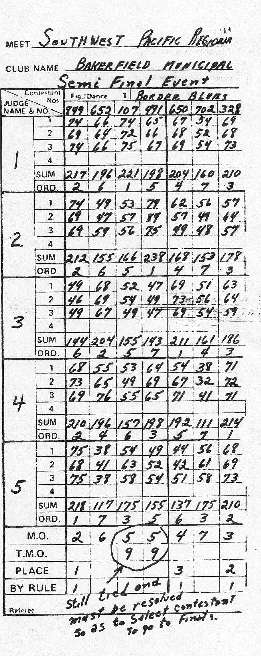Part III appeared in the previous issue of Round and Round and outlined the procedure used for assigning the majority ordinal (MO) and the application of Rule 1 for awarding the highest open placement. In Part III, you will recall that after awarding first, second and third places, we ended with two contestants having the same MO's tied for fourth place. This tie situation must be resolved by successive application of Rules 2 through 11. If the tie cannot be broken by one of these rules a re-skate may result.

You will note that the sample score sheet printed here is a reproduction of that used in Part III with the additional tie breaking rules applied.

Where the highest open place cannot be awarded by Rule 1, which is the case we have here, a Total Majority Ordinal (TMO) must be computed for each contestant having the same low MO for the place in question. The TMO is the number obtained by adding the ordinals which where used for forming the MO. Remember from Part III that the ordinals used for forming the MO were the best or lowest three out of five MO's. It is these three that we just sum to obtain the TMO. After obtaining the TMO's for the tied contestants and entering them on the score sheet in the respective box of the TMO line. Rule 2 is applied. Note on our sample score sheet that both contestants with the MO's of 5 have TMO's of 9 which were obtained in both cases from the sum of the best three out of five ordinals, 1, 3, and 5.

Rule 2 states that the contestant involved in the tie that has the lowest total majority ordinal (TMO) shall be awarded the place in question. When applying this rule to our sample problem, you will notice, however that the TMO's for both contestants are nine which means that these contestants are still in a tied situation. When Rule 2 will not result in a placement decision, the ties will fall in one of the two following categories: (1) ties not affecting the number contestants qualified to skate in the next higher event, (i.e., Quarter Finals, Semi-Finals, or Finals, or (2) ties affecting the number of contestants qualified to skate in the next higher event. All ties under category (1) are covered by Rule 3, which states that ties not affecting the number of contestants permitted to skate in the next higher event shall remain tied for the place in question. Hence, if our sample problem was the result of an elimination event and 8 contestants were to be selected for the semi-final event, then the tied contestants would both qualify for the semi-finals and would be assigned a tied fourth place under Rule 3. If however, the sample problem was the result of a semi-final event, where the first four placements would qualify to skate in the final event, it would be necessary to resolve the time to determine which of the contestants qualified to skate. This case would fall under category (2) and require application of Rule 4 for a possible solution.

It is interesting to tone that up to this point the placement decision involves only those judges that provided the best three out of the five ordinals, or putting it another way, involved only the majority judges. However when Rule 4 and higher are required to resolve a tie, all judges' scores or ordinals will come into play.

In order to apply Rule 4, it will be necessary to look at all judges' individual scores, but we have just run out of space in this issue and must defer resolution of our sample problem tie until the next issue of Round and Round. Be sure to get your copy and follow this important area of scoring.

Part V

P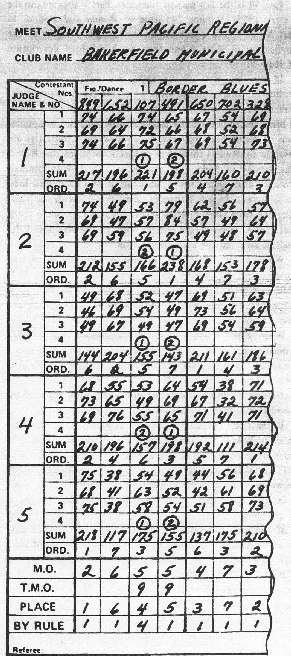art IV of this article appeared in the Fall 1975 (Volume 23) issue of Round and Round. In part IV, we covered the application of Rule 3 to our sample problem and determined that it would be necessary to apply higher rules for its solution.

In this issue we will continue with the application of Rule 4 to the sample problem and see if this rule will yield a placement decision. In order to apply Rule 4, the SUMS of the contestants with the Majority Ordinal (MO) and Total Majority Ordinal (TMO) shall be set aside on a separate "work Sheet" and the SUMS re-ordinaled as if they had competed in a separate contest. After re-ordinaling, the re-ordinaled 1's are added. We are not prepared to apply rule 4. Rule 4 states that "the involved contestant with the greater number or re-ordinal 1's shall be awarded the place in question." Due to lack of space, we are unable to print a sample work sheet here, but instead we will mark the re-ordinaled numbers just above the SUMS on our sample score sheet.

A look at the sample score sheet will show that contestant 107 had a total of three re-ordinal 1's while contestant 491 had two re-ordinal 1's. This means that contestant 107 has, in general, better scores than contestant 491 and will receive the placement in question according to rule 4.

With the awarding of the 4^th place by the process shown above, contestant 491 is no longer involved in a tie and may be awarded the 5^th place according to Rule 1. Now that the tie is resolved, you should observe that contestants 849, 107, 650, and 328 qualify for the final event.

By in large, most ties are resolved by Rules 1, 2 or 3 and do not necessitate the application of Rule 4 or higher. However ties to happen frequently enough to warrant an understanding of Rule 4.

If, when re-ordinaling the SUMS in preparation for preparation for Rule 4 results in and equal number of 1's (i.e., two contestants having the same SUM), the tie cannot be resolved by Rule 4 and must be carried forward for application of Rule 5. In preparation for the application of Rule 5, the individual scores (IS) of the two or more tied contestants shall be listed on the same work sheet that was used for Rule 4 and ordinal all individual scores of the two or more involved contestants. From these individual score ordinals (ISO) a Majority Ordinal (ISO-MO) is obtained by using the same process we did in Part III. After obtaining the ISO-MO, we are ready to apply Rule 5. Rule 5 states that "the involved contestant with the lowest Individual Score Ordinaling Majority Ordinal (ISO-MO) shall be awarded the place in question." This rule simply means that the contestant with the larger number of higher individual scores will receive the better placement. Rule 5 is very similar to Rule 1. The difference being that Rule 1 deals with the Majority Ordinals obtained from the contestant's SUMS while Rule 5 deals with the Majority Ordinals obtained from the individual scores.

Part VI will be published in the next issue of Round and Round and will be the last part of the series. It will briefly outline Rules 6 through 11. The discussion of each rule will be brief because the application of these rules is seldom required. Be sure to get your copy of the next important issue so that your series will be complete with all six articles.

Part VI

Part VI is the last part of the series. Part V appeared in the Winter 1975 (Volume 24) issue of Round and Round. In Part V we found a solution of our sample problem by the application of Rule 4 and then we had a brief description of Rule 5.

In this last part of the series, we will provide a brief outline of Rules 6 through 11, which are the remaining rules utilized when necessary to determine a tie-breaking placement. A brief description will be provided only because the application of these rules are seldom required since most ties are resolved by Rules 1 through 5. In Part V we stated that Rule 5 was similar to Rule 1 in that Rule 1 deals with ordinals obtained from the individual SUMS while Rule 5 deals with individual scores. In a like manner, Rule 6 deals with the TMO obtained from the individual scores (ISO-TMO). Rule 6 states that "The involved contestant with the lowest ISO-TMO shall be awarded the place in question."

When a tie cannot be resolved by Rule 6, individual score ordinals are totaled on the same worksheet as the ISO-TMO and Rule 7 is applied. Rule 7 states that "The involved contestant with the lowest ISO-TO shall be awarded the place in question."

When Rule 7 will not provide a solution, the original ordinals assigned to the SUMS of each of the tied contestants are added to obtain a TOTAL ORDINAL (TO) value. This provides the information necessary to apply Rule 8. Rule 8 states that "The involved contestant wit the lowest TO shall be awarded the place in question."

If the tied contestants have the same TO, it is necessary to apply Rule 9. In order to apply Rule 9, the SUM that each judge assigned to the tied contestant is added to obtain a point total (PT) figure. Rule 9 states that "The involved contestant with the highest PT shall be awarded the place in question."

In the event that application of Rule 9 will not provide a solution to the tie, the SUMS of the tied contestants are re-ordinaled as if the had competed in a separate contest. The number of re-ordinal 1's are counted for each tied contestant and Rule 10 applied Rule 10 states that "The involved contestant greatest number of re-ordinal 1's shall be awarded the place in question." This rule may seem to be a duplication of Rule 4 outlined in Part V and, in fact, it is the same. However, remember that during the process of applying each succeeding rule, a contestant, in a case where there is three or more tied contestants my be removed from the tied status by either of Rules 5 through 9 and, in this case, the re-ordinal 1's could provide new information.

When the tie cannot be resolved by application of Rule 10. The two or more involved contestants with the same number of re-ordinal 1's will remain tied and fall into one of the two categories of Rule 11. These categories are: (a) ties affecting the awarding of a 1^st, 2^nd, or 3^rd place award, or affecting the number of contestants permitted to skate a final event, then the involved contestants shall re-skate under the competitive rules of their division. (b) Ties affecting the number of contestants permitted to skate in a quarter-final or semi-final event; these involved contestants also shall qualify to compete in the next higher event.

The eleven rules outlined in this series constitute the entire set of rules used for tie breaking. As mentioned before, Rules 5 through 11 are seldom used, in f act, I personally have not seen a tie involving a re-skate.

Admittedly, this series has been somewhat brief. However it was not intended to be used to train qualified tabulators. If the readers have found the information provided sufficient to enable them to read the posted score sheets, then the objective of the article has been fulfilled.

For the reader who would like a more detailed understanding, the USAC has published a booklet entitled "Tabulating Scoring Manual" which may be obtained from your rink or the USAC National Office, Lincoln, Nebraska. For those who would like to become tabulators, a study guide should be available from your rink teaching staff.